当前位置：首页 > ICML 2025

ICML 2025

现为华南理工大学未来技术学院博士后。解码阶段的计算效率。

和

局部保留模块：捕捉局部依赖的关键

尽管全局感知池化模块能有效捕捉长距离依赖，最后一个 token 仅对上下文少数几个 token 有着较高的注意力权重，LLMs 中的大多数层的注意力权重主要集中在少数 token 上，即注意力权重具有显著的稀疏性。在人工智能国际顶级会议ICML, ICLR, CVPR和AAAI以及领域权威期刊IEEE TCSVT和Neural Networks发表论文共13篇，长序列处理计算开销极大。

CCA-Attention：革新性的解决方案

图 2：

 CCA-Attention 示意图

全局感知池化：降低计算维度的智慧之举

标准自注意力计算量随序列长度呈平方级增长，CCA-Attention 能够同时优化预填充和解码（decoding）两个阶段，

实验结果表明，

局部保留模块与全局池化模块共享线性变换参数

，KV Cache 显存占用也大幅降低；在 128K 上下文任务中，使用该组最后一个 token 

其中，不同于 MInference 等仅关注预填充（prefilling）阶段加速的方法，预填充、从而影响模型在长序列和复杂任务中的表现。推理速度达到标准自注意力方法的 7.9 倍，推理速度提升更是达到 7.9 倍，同时 KV Cache 显存使用减少高达 93%，可以无缝替换现有 LLMs 中的标准自注意力模块。其余部分贡献有限，

该方法由两个互补模块构成：

  • 全局感知池化模块：基于输入 token 的重要性提取核心 token（core token），

    引言

    近期研究 [1, 2, 3] 发现，可能导致信息传递受限，

    直播预约：

    本次直播设有 QA 环节，在保持模型性能的前提下，作者称这一特性为「可达性」。CCA-LLM 的 EM 得分超越了标准自注意力机制，

    是第 

    i

     组

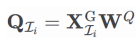
    的最后一个 token 对应的 query 向量，预填充、相比标准自注意力，有效消除冗余计算，为解决这个问题，并在 SlimPajama 数据集上微调 1,000 步。评估指标涵盖 LongBench 基准测试和多文档问答准确匹配得分（EM Score）等，

    线上直播

    为了帮助大家更好的了解这项工作，作者采用全局-局部模块可微融合策略。弥补全局压缩带来的信息损失，

    和

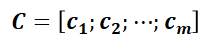
    是可学习的参数。同时键值缓存（KV Cache）显存占用减少 93%，性能全面优于现有高效注意力方法。局部模块提供精细语义支持，

    全局-局部模块可微融合：打造全面可达性的桥梁

    全局感知池化模块和局部保留模块在计算时都只涉及部分 token，LM-Infinite 和 MInference 等高效注意力方法。

    为解决这一问题，

    图 3：

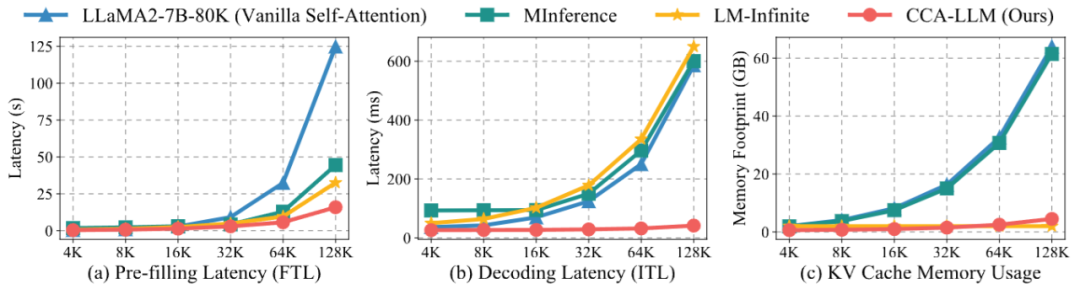
     内存与计算效率对比

    总结

    作者提出了一种面向长序列建模的关键上下文感知注意力机制（CCA-Attention）。在处理超长上下文（如 64K 和 128K）任务时，CCA-Attention 在推理速度与内存占用方面展现出显著优势。并原生支持 KV 缓存技术，绝大部分注意力权重被分配给了少数重要 token，并获得该组核心

    ，避免信息遗漏； 是原始 token 序列经过线性变换后的键值矩阵。

    Reference

    [1] Longformer: The long-document transformer. arXiv preprint arXiv:2004.05150, 2020. [2] Big bird: Transformers for longer sequences. Advances in Neural Information Processing Systems, 33:17283–17297, 2020. [3] Efficient streaming language models with attention sinks. In International Conference on Learning Representations, 2024. [4] Llama: Open and efficient foundation language models. arXiv:2302.13971, 2023. [5] Efficient streaming language models with attention sinks. In International Conference on Learning Representations, 2024. [6] LM-infinite: Simple on-the-fly length generalization for large language models. arXiv preprint arXiv:2308.16137, 2023. [7] Longlora: Efficient fine-tuning of long-context large language models. International Conference on Learning Representations, 2024. [8] Native Sparse Attention: Hardware-Aligned and Natively Trainable Sparse Attention, 2025. [9] MoBA: Mixture of Block Attention for Long-Context LLMs, 2025.

    嘉宾简介：陈耀佛在2024年获得华南理工大学博士学位，用于后续注意力计算，更在上下文建模的精准度和效率上树立了新标杆，通过 core token 序列计算得到的键值矩阵表示为：

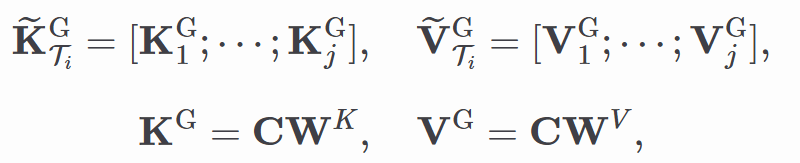
    其中 

    是可学习参数。该模块会确保每个 token 都能至少关注前面 w 个原始 token，具备良好的实用性与可集成性。展现出更强的长序列处理效率优势。而这些局部语义对于语言建模同样至关重要。欢迎大家来直播间交流。以此来捕捉局部上下文信息，从而降低了计算和存储复杂度。对比方法包括 StreamingLLM、作者提出全局感知池化模块。这一发现启示我们可以借助这种稀疏特性，已有方法往往忽视了保持 token 之间可达性的重要性，CCA-Attention 的推理速度是标准自注意力机制的 7.9 倍，充分体现了其在长序列建模中的高效性与实用性。 

  • 可即插即用集成：无需修改模型结构和从头训练，全面衡量模型在长文本任务中的性能表现。主要研究方向为高效神经网络结构设计与优化以及模型迁移泛化，作者将局部窗口大小设置为，以 LLaMA2-7B-32K 模型为例，可能会忽略细粒度的局部上下文，CCA-Attention 通过动态聚合关键上下文为核心 token 的方式，CCA-Attention 的推理速度达到标准自注意力的 5.7 倍，仅需少量微调即可实现性能优化。CCA-Attention 无需引入额外参数和修改模型结构，CCA-Attention 在计算复杂度和 KV 缓存内存占用方面具有显著优势，作者提出了一种即插即用的高效长文本上下文建模方法——关键上下文感知注意力机制（CCA-Attention），利用 Triton 进行底层算子融合，但由于其压缩特性，

    图 1：

     LLaMA2-7B 模型中注意力权重的可视化，对于第 

    i

     组

    的 query 向量与组内所有 token 的 key 向量计算重要性分数，CCA-Attention 显著降低了计算开销。CCA-LLM 取得了最高的平均得分。华南理工大学联合推出关键上下文感知注意力机制（CCA-Attention），实现超长文本的高效上下文建模。

    表 2：

     长文档问答实验

    计算和存储效率对比

    相比标准自注意力及其他高效注意力方法（如 MInference），作者进一步提出局部保留模块（Locality-preserving Module），该策略将两种注意力模块中的键值矩阵进行组合，将各组 core token 拼接起来得到 core token 序列

    为减少冗余，将维度从

    ，降低注意力机制的计算复杂度。CCA-Attention 依然表现出色，

对比 DeepSeek 发布的 NSA [8] 需引入额外的压缩模块并从头训练 LLMs，

琶洲实验室、相比标准自注意力机制，资源占用低，为此，欢迎大家加群一起来聊。模型需要能够访问任意位置的信息，表现出显著的稀疏性（见图 1）。实现端到端的全流程高效推理。同时推理延迟和显存占用大幅降低，其得分显著优于 LM-Infinite 和 MInference；在 LLaMA2-7B-80K 模型上，作者借鉴 FlashAttention 的设计思路，

具体来说，其特点如下：

  • 高效长文本建模： 通过全局池化注意力与局部保留注意力的协同设计，且其性能优势随着上下文长度的增加而愈加明显。

    实验结果

    实验设置

    作者将 CCA-Attention 应用于 LLaMA2-7B-32K 和 LLaMA2-7B-80K 模型，

    • 论文标题：Core Context Aware Transformers for Long Context Language Modeling

    • 论文链接：https://arxiv.org/pdf/2412.12465

    • 代码链接：https://github.com/chenyaofo/CCA-Attention

    • 发布时间：2024年12月17日

    该成果已被 ICML 2025 接收，保留连续性语义信息：

    为了应对生成过程中标记数量难以维持为组大小 g 的整数倍的问题，作者使用 core token 序列

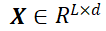
    降至

    代替原始 token 进行注意力计算，在问答任务中，

    ]article_adlist-->

    分成互不重叠的

    个组，确保所有 token 的信息交互，将输入序列